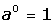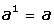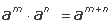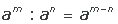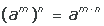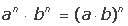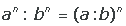Criptografía
¿Qué
es?
Criptografía
(literalmente «escritura oculta»)es un término genérico que
describe todas las técnicas que permiten cifrar mensajes o hacerlos
ininteligibles sin recurrir a una acción específica. El verbo
asociado es cifrar. Se basa en la aritmética.
Si
se intenta descifrar el mensaje sin conocer la clave y sin permiso
del remitente hablamos de criptoanálisis.
La
criptología es la ciencia que estudia los aspectos científicos de
estas técnicas, es decir, combina la criptografía y el
criptoanálisis.
En
nuestros días, en el caso de un texto, consiste en transformar las
letras que conforman el mensaje en una serie de números (en forma de
bits ya que los equipos informáticos usan el sistema binario) y
luego realizar cálculos con estos números para:
-Modificarlos
y hacerlos incomprensibles para cualquiera que no tenga la clave de
cifrado.
-Asegurarse
que solo el receptor pueda descifrarlos.
Las
claves de cifrado pueden ser de dos tipos:
Simétricas:
son las claves que se usan tanto para el cifrado como para el
descifrado. En este caso hablamos de cifrado simétrico o cifrado con
clave secreta.
Asimétricas:
son las claves que se usan en el caso del cifrado asimétrico
(también llamado cifrado con clave pública). En este caso, se usa
una clave para el cifrado y otra para el descifrado.
Cuando
nos conectamos a servicios como Gmail, estamos estableciendo una
comunicación segura y, por tanto, cifrada entre nuestro ordenador (o
nuestro dispositivo móvil) y los servidores de Google. Cuando
realizamos una llamada telefónica desde nuestro terminal móvil, la
secuencia de datos que generamos también está cifrada y, de esta
forma, se evita que alguien no autorizado pueda estar a la escucha e
interceptar nuestras comunicaciones.
Métodos
de la antigüedad:
Este
arte se remonta a mucho antes de los habituales referentes, Alan
Turing o la NSA, ya en la Biblia se hace refencia a un sistema de
sustitución de letras llamado Atbash. También en la Ilíada de
Homero se hace referencia al cifrado de mensajes.
Los
espartanos también usaban la criptografía para proteger sus
mensajes; concretamente, una técnica que consistía en enrollar un
pergamino sobre una estaca (llamada escítala) que servía para
ordenar las letras y mostrar el mensaje. Para poder descifrarlo, el
receptor debía contar con una escítala del mismo diámetro que la
que había usado el emisor (criptografía simétrica) porque era la
única forma de visualizar el mensaje de la misma forma.
De
la Antigua Roma procede el conocido como cifrado
César
que, como bien indica su nombre, su uso se atribuye al mismo Julio
César. Este cifrado se basa en el desplazamiento de letras y, por
tanto, cada letra del texto original se sustituye por otra letra. En
este caso se usaba un desplazamiento de tres letras.
En
el siglo IX, Al-Kindi sentaría una de las bases fundamentales para
"romper mensajes cifrados" gracias al estudio del Corán;
el análisis
de frecuencia
(una técnica que se usó durante la Segunda Guerra Mundial) se
basaba en analizar patrones en los mensajes cifrados para localizar
repeticiones y buscar la correlación con la probabilidad de que
aparezcan determinadas letras en un texto escrito en un idioma
concreto.
En
el Renacimiento tiene su origen el que sigue siendo "el gran
reto" de los descifradores de códigos: el Manuscrito
Voynich,
un libro cuyo contenido es aún ininteligible y cuyo código no se ha
podido romper.
Durante
la Segunda Guerra Mundial:
La
criptografía fue clave durante la Segunda Guerra Mundial y, de
hecho, hizo cambiar el curso de la guerra. Alemania había conseguido
dominar el Atlántico Norte y sus comunicaciones eran indescifrables
gracias a la máquina Enigma.
Quizás
el trabajo de Alan Turing y los Aliados sea la labor más conocida
sobre criptografía durante la Segunda Guerra Mundial; sin embargo no
fue el único. El
Cuerpo de Marines de Estados Unidos contaba entre sus filas con medio
millar de nativos americanos que servían como operadores de radio y
cifraban, en su lengua nativa, los mensajes a transmitir para que el
ejército japonés no pudiese entender nada de lo que se transmitía.
Después
de la segunda guerra mundial:
Después
de la Segunda Guerra Mundial, la criptografía dio un gran salto
gracias a Claude Shannon, conocido como el padre de la teoría de la
comunicación. Si bien es cierto que el análisis de frecuencia se
basaba en la estadística, Shannon demostró matemáticamente este
hecho e introdujo el concepto de “distancia de unicidad” que
marcaba la longitud de un texto cifrado que se necesita para poder
descifrarlo.
La
explosión de la computación convirtió a los computadores en un
instrumento clave dentro del cifrado y descifrado de mensajes; por
tanto, por seguridad, la mayoría de países consideraron la
criptografía
como algo secreto,
vinculado
a tareas de inteligencia y espionaje. Desde mediados de los años 50
hasta mediados de los 70, la
NSA acaparó y bloqueó cualquier tipo de publicación o estudio
sobre criptografía
en Estados Unidos.
Hasta
el 17 de marzo de 1975 no llegaría el primer "avance público".
IBM desarrolló el algoritmo de cifrado Data Encryption Standard
(DES) que, dos años más tarde, se convertiría en un Federal
Information Processing Standard (FIPS 46-3) y se extendería su uso
por todo el mundo. En el año 2001, DES cedería su puesto a Advanced
Encryption Standard (AES)
que, tras 5 años de revisión, se convirtió en un estándar. En los
años 70 también se descubrió la criptografía asimétrica,
hoy fundamental para transacciones realizadas a través de Internet,
por ejemplo, en páginas que usan el protocolo HTTPS o para cifrar
nuestros mensajes usando PGP (que combina tanto criptografía
asimétrica como criptografía asimétrica).





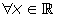
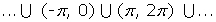
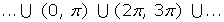

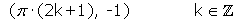
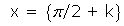


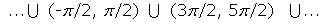
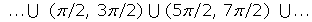
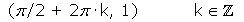
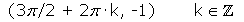
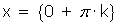













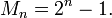
 , con n primo (no es una condición suficiente que n sea primo para que
, con n primo (no es una condición suficiente que n sea primo para que  lo sea).
lo sea).
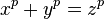 .
.