Abu Jafar Muhammad (Musa Al-Jwarizmi)
Nació alrededor del 780 d.C. en Jorezm, al sur del Mar de Aral (hoy Jiva, Uzbekistán), que había sido conquistado 70 años antes por los árabes. Era árabe con antecedentes indios y babilonios. Su nombre ya dice mucho, pues significa "Mohamed, hijo de Moisés, padre de Jafar, el de Khorezm". Su fama debió ser muy grande para que todo el mundo lo conociera por su lugar de origen. Hacia el 820, Al-Jwarizmi fue llamado a Bagdad por el califa abasida Al-Mamun, segundo hijo de Harun ar-Rashid, por todos conocido gracias a las Mil y unas Noches. Al-Mamun continuó el enriquecimiento de la ciencia árabe y de la Academia de Ciencias creada por su padre, llamada la Casa de la Sabiduría, lo que traería importantes consecuencias en el desarrollo de la ciencia en Europa, principalmente a través de España. Falleció en Bagdad hacia el 850 d.C
Al-Jwarizmi fue un recopilador de conocimiento de los griegos y de la India, principalmente matemáticas, pero también astronomía (incluyendo el calendario Judío), astrología, geografía e historia. Su obra se influenció particularmente de los escritos de Diofanto. Palabras como “álgebra”, “guarismo” o “algoritmo” las debemos a su nombre y al de su principal obra, “hisab al yabr ua al maqabala”. De hecho, se le considera como el padre del álgebra y como el iniciador de nuestro sistema de numeración.
Su trabajo más conocido y usado fueron sus Tablas Astronómicas, basadas en la astronomía india. Incluyen algoritmos para calcular fechas y las primeras tablas conocidas de las funciones trigonométricas seno y cotangente. Lo más increíble es que no usó los números negativos (que aún no se conocían), ni el sistema decimal ni fracciones. Su aritmética introduce el sistema numérico indio (sólo conocido por los árabes unos 50 años antes) y los algoritmos para calcular con él.
Finalmente tenemos el Álgebra, una introducción compacta al cálculo, usando reglas para completar y reducir ecuaciones. Además de sistematizar la resolución de ecuaciones cuadráticas, también trata geometría, cálculos comerciales y de herencias.
Evariste Galois
Con sólo dieciseis años, interesado en hallar las condiciones necesarias para definir si una ecuación algebraica era susceptible de ser resuelta por el método de los radicales, empezó a esbozar lo que más adelante se conocería con el nombre genérico de «teoría de Galois», analizando todas las permutaciones posibles de las raíces de una ecuación que cumplieran unas condiciones determinadas.
Mediante dicho proceso, que en terminología actual equivale al de hallar el grupo de automorfismos (Que es, en términos generales, el grupo de simetría del objeto) de un cuerpo, sentó las bases de la moderna teoría de grupos, una de las ramas más importantes del álgebra. Galois intuyó que la solubilidad mediante radicales estaba sujeta a la solubilidad del grupo de automorfismos relacionado.
A pesar de sus revolucionarios descubrimientos, o tal vez por esa misma causa, todas las memorias que publicó con sus resultados fueron rechazadas por la Academia de las Ciencias.
Se vio implicado en un duelo cuyas motivaciones aún hoy permanecen confusas. Previendo su más que posible muerte en el lance, trabajó febrilmente en una especie de testamento científico que dirigió a su amigo Auguste Chevalier. A los pocos días tuvo lugar el duelo y el matemático, herido en el vientre, murió unas horas después, apenas cumplidos los veintiún años.
Carl Friedrich Gauss
El 4 de mayo de 1777 el viejo párroco de Wendengraben, en Brunswick, Alemania, procede a inscribir a un nuevo feligrés: Johann Friedrich Carl; se trata de un niño varón, nacido cuatro días antes, el último día del mes de abril, el hijo de un humilde matrimonio, la pareja formada por Geghard Dietrich Gauss y Dorothea Benze, ambos de 33 años.A los siete años, tras serios esfuerzos de Dorothea para convencer al padre, Gauss ingresa en la escuela primaria. A los nueve años Gauss asiste a su primera clase de Aritmética. Büttner propone a su centenar de pupilos un problema terrible: calcular la suma de los cien primeros números. Nada más terminar de proponer el problema, el jovencito Gauss traza un número en su pizarrín y lo deposita en la mesa del maestro exclamando: “Ligget se!” (¡Ahí está!). Había escrito 5.050. La respuesta correcta. Se había dado cuenta de que la suma de la primera y la última cifra daba el mismo resultado que la suma de la segunda y la penúltima, etc., es decir: 1+ 100 = 2 + 99 = 3 + 98 = ... = 101
Con 11 años de edad Gauss dejará la Katherinen Volkschule para ingresar en el Gymnasium Catharineum. Allí estudia latín y griego y al cabo de dos años accede al grado superior de la enseñanza secundaria. Su fama se empieza a extender por los círculos cultivados de Brunswick y llegará a oídos del duque Karl Wilhelm Ferdinan. Éste le recibe en audiencia, Gauss es un adolescente de 14 años que deja impresionado al anciano duque con su habilidad de cálculo. El duque le proporcionará los fondos para que pueda proseguir su formación y le regalará las tablas de logaritmo.
Cuando en el otoño de 1795 se traslada a la Universidad Georgia Augusta de Göttingen, con una beca del Duque. Gauss aún no ha decidido su futuro académico dudando entre los estudios de Filología clásica y las Matemáticas. Justo un mes antes de cumplir los 19 años, Gauss se decantará definitivamente por las matemáticas y hará su primera anotación en su diario de notas, un pequeño cuaderno de 19 páginas, que acompañará a Gauss hasta 1814.
A esta edad Gauss halló un método para construir un polígono equilátero de 17 lados con ayuda de regla y compás, e incluso fue más allá, demostrando que sólo ciertos polígonos equiláteros se podían construir con ayuda de regla y compás.
En 1799 Gauss demostró el teorema fundamental del álgebra, que afirma que toda ecuación algebraica tiene una raíz de la forma a+bi donde a y b son números reales, e i es la unidad imaginaria.
- También demostró que los números se podían representar mediante puntos en un plano.
- El 1801 demostró el teorema fundamental de la aritmética: todo número natural se puede representar como el producto de números primos de una y solamente una forma.
- Durante su estancia en el observatorio, construyó un heliotropo, instrumento que reflejaba la luz solar a grandes distancias.
- Uno de sus principales descubrimientos fue la campana de gauss
En matemáticas, la campana de Gauss es la representación gráfica de la ecuación matemática a una distribución normal. Tiene forma de campana. .Si se representa en el eje horizontal las medidas obtenidas y en el vertical el número de veces que se obtiene cada valor, obtendremos lo que se llama un histograma de frecuencias. Si se elimina el error sistemático, el conjunto de datos obtenido se distribuye de forma simétrica alrededor de la media, dando una curva en forma de campana.
Algunas de sus aportaciones menos conocidas:
- Teoría de los errores.
- Método general para la resolución de las ecuaciones binomios.
- Ideó un heliotropo, para el envío de señales luminosas en las operaciones geodésicas (operaciones de mediciones terrestres).
- Formuló la Teoría general del magnetismo terrestre.
- Campana de Gauss que es muy utilizada en el cálculo de probabilidades.
- Realizó aportaciones en la electricidad y en el magnetismo.
- El teorema de Gauss-Bonnet
- El método de Gauss para triangular una matriz (y el método de eliminación de Gauss-Jordan).
- El método de Gauss-Seidel (método iterativo para resolver sistemas de ecuaciones lineales).
- El teorema de la divergencia, conocido también como teorema de Gauss (y por teorema de Ostrogradsky-Gauss).


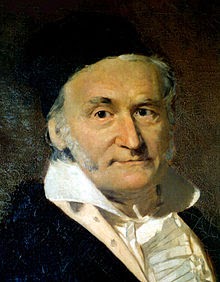

No hay comentarios:
Publicar un comentario